Superficie de Scherk

En matemáticas, una superficie de Scherk, nombre en honor al matemático alemán Heinrich Scherk, es un ejemplo de superficie mínima. Scherk describió dos superficies mínimas embebidas completas en 1834.^[1]​ La primera es una superficie doblemente periódica, y la segunda es individualmente periódica. Fueron el tercer ejemplo no trivial de superficie minimal, siendo los dos primeros fueron el catenoide y el helicoide.^[2]​ Las dos superficies son conjugadas entre sí.

Las superficies de Scherk surgen en el estudio de ciertos problemas de superficies mínimas limitantes y en el estudio de difeomorfismos armónicos del espacio hiperbólico.

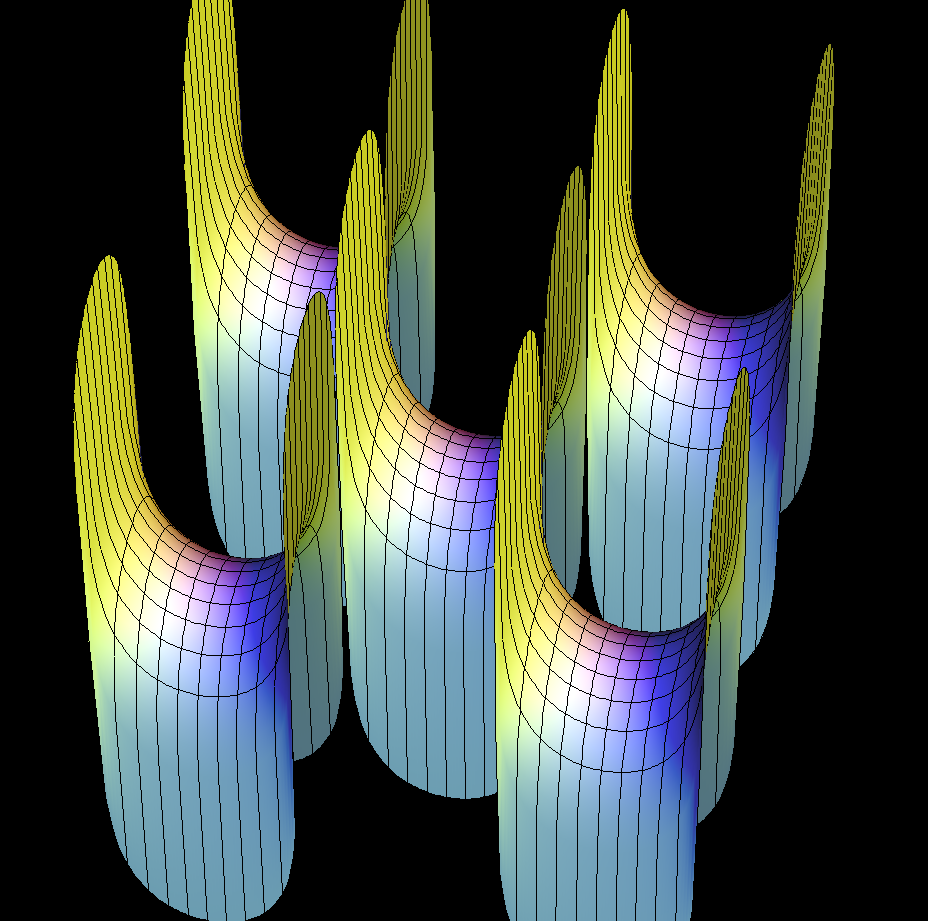
La primera superficie de Scherk

La primera superficie de Scherk es asintótica a dos familias infinitas de planos paralelos, ortogonales entre sí, que se encuentran cerca de z=0 en un patrón de tablero de ajedrez de arcos puente. Contiene un número infinito de líneas verticales rectas.

Construcción de una superficie Scherk simple

Considérese el siguiente problema de superficie mínima en un cuadrado en el plano euclídeo: para un número natural n dado, encontrar una superficie mínima Σ_n como gráfica de alguna función

${\displaystyle u_{n}:\left(-{\frac {\pi }{2}}, {\frac {\pi }{2}}\right)\times \left(-{\frac {\pi }{2}}, {\frac {\pi }{2}}\right)\to \mathbb {R} }$

tal que

${\displaystyle \lim _{y\to \pm \pi /2}u_{n}\left(x,y\right)= n{\text{ si }}-{\frac {\pi }{2}}$

${\displaystyle \lim _{x\to \pm \pi /2}u_{n}\left(x,y\right)=-n{\text{ si }}-{\frac {\pi }{2}}$

Es decir, u_n satisface la condición de superficie mínima

${\displaystyle \mathrm {div} \left({\frac {\nabla u_{n}(x,y)}{\sqrt {1 |\nabla u_{n}(x,y)|^{2}}}}\right)\equiv 0}$

y

${\displaystyle \Sigma _{n}=\left\{(x,y,u_{n}(x,y))\in \mathbb {R} ^{3}\left|-{\frac {\pi }{2}}$

¿Cuál es, en todo caso, la superficie límite cuando n tiende a infinito? La respuesta la dio H. Scherk en 1834: la superficie límite Σ es la gráfica de

${\displaystyle u:\left(-{\frac {\pi }{2}}, {\frac {\pi }{2}}\right)\times \left(-{\frac {\pi }{2}}, {\frac {\pi }{2}}\right)\to \mathbb {R} ,}$

${\displaystyle u(x,y)=\log \left({\frac {\cos(x)}{\cos(y)}}\right).}$

Es decir, la superficie de Scherk sobre el cuadrado es

${\displaystyle \Sigma =\left\{\left.\left(x,y,\log \left({\frac {\cos(x)}{\cos(y)}}\right)\right)\in \mathbb {R} ^{3}\right|-{\frac {\pi }{2}}$

Superficies de Scherk más generales

Se pueden considerar problemas de superficie mínima similares en otros cuadriláteros en el plano euclídeo. También se puede considerar el mismo problema con cuadriláteros en el plano hiperbólico. En 2006, Harold Rosenberg y Pascal Collin utilizaron superficies hiperbólicas de Scherk para construir un difeomorfismo armónico desde el plano complejo al plano hiperbólico (el disco unitario con la métrica hiperbólica), refutando así la conjetura de Schoen-Yau.

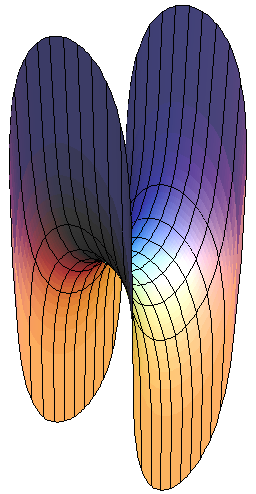
Segunda superficie de Scherk

La segunda superficie de Scherk se asemeja globalmente a dos planos ortogonales cuya intersección consiste en una secuencia de túneles en direcciones alternas. Sus intersecciones con planos horizontales consisten en hipérbolas alternas.

Tiene ecuación implícita:

${\displaystyle \sin(z)-\sinh(x)\sinh(y)=0}$

y su parametrización de Weierstrass-Enneper tiene la forma ${\displaystyle f(z)={\frac {4}{1-z^{4}}}}$, ${\displaystyle g(z)=iz}$; y se puede parametrizar como:^[3]​

${\displaystyle x(r,\theta )=2\Re (\ln(1 re^{i\theta })-\ln(1-re^{i\theta }))=\ln \left({\frac {1 r^{2} 2r\cos \theta }{1 r^{2}-2r\cos \theta }}\right)}$

${\displaystyle y(r,\theta )=\Re (4i\tan ^{-1}(re^{i\theta }))=\ln \left({\frac {1 r^{2}-2r\sin \theta }{1 r^{2} 2r\sin \theta }}\right)}$

${\displaystyle z(r,\theta )=\Re (2i(-\ln(1-r^{2}e^{2i\theta }) \ln(1 r^{2}e^{2i\theta }))=2\tan ^{-1}\left({\frac {2r^{2}\sin 2\theta }{r^{4}-1}}\right)}$

para ${\displaystyle \theta \in [0,2\pi )}$ y ${\displaystyle r\in (0,1)}$. Esto da un período de la superficie, que luego puede extenderse en la dirección z por simetría.

H. Karcher ha generalizado la superficie en la familia de la torre de sillas de montar de superficies mínimas periódicas.

De manera algo imprecisa, esta superficie se denomina ocasionalmente la quinta superficie de Scherk en la bibliografía.^[4]​^[5]​ Para minimizar la confusión, es útil referirse a ella como superficie periódica única de Scherk o torre de Scherk.

Enlaces externos

• Sabitov, I.Kh. (2001), «Superficie de Scherk», en Hazewinkel, Michiel, ed., Encyclopaedia of Mathematics (en inglés), Springer, ISBN 978-1556080104 .
• Primera superficie de Scherk en geometría MSRI [2]
• Segunda superficie de Scherk en Geometría MSRI [3]
• Superficies mínimas de Scherk en Mathworld [4]

Referencias